description for the article
De plusieurs façons, On peut définire un plan dans l'espace :
- À travers trois points A, B, C non alignés de l'espace : le plan est dans ce cas, l'ensemble des points M de l'espace tels que \(\overrightarrow{A M}= a \overrightarrow{A B}+ b \overrightarrow{A C}\) ou a et b des nombres réels. Les vecteurs \(\overrightarrow{A B}\) et \(\overrightarrow{A C}\) sont parfois appelés vecteurs directeurs du plan.
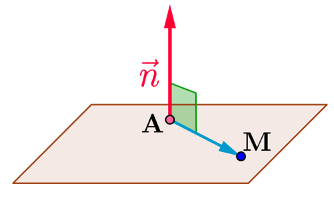
- À travers un point \(A\) et un vecteur normal \({\vec{n}}\) au plan, le plan est dans ce cas l'ensemble des points \(M\) tels que les vecteurs \(\vec{A} \vec{M}\) et \({\vec{n}}\) sont orthogonaux.
Definition 1 : Soient \(\vec{u}(x ; y ; z), \vec{v}\left(x^{\prime} ; y^{\prime} ; z^{\prime}\right)\) et \(\vec{w}\left(x^{\prime \prime} ; y^{\prime \prime} ; z^{\prime \prime}\right)\) trois vecteurs de l'espace muni d'une base \((\vec{i} ; \vec{j} ; \vec{k})\). Le déterminant des vecteurs \(\vec{u}, \vec{v}\) et \(\vec{w}\) dans cet ordre est le réel noté \(\operatorname{det}(\vec{u} ; \vec{v} ; \vec{w})\) et défini par : |
Theoreme 1 : Soient \(\vec{u}(x ; y ; z), \vec{v}\left(x^{\prime} ; y^{\prime} ; z^{\prime}\right)\) et \(\vec{w}\left(x^{\prime \prime} ; y^{\prime \prime} ; z^{\prime \prime}\right)\) trois vecteurs de l'espace muni d'une base \((\vec{i} ; \vec{j} ; \vec{k})\). Le déterminant des vecteurs \(\vec{u}, \vec{v}\) et \(\vec{w}\) dans cet ordre est le réel noté \(\operatorname{det}(\vec{u} ; \vec{v} ; \vec{w})\) et défini par : |
Exercice 1 : Soient \(\vec{u}(x ; y ; z), \vec{v}\left(x^{\prime} ; y^{\prime} ; z^{\prime}\right)\) et \(\vec{w}\left(x^{\prime \prime} ; y^{\prime \prime} ; z^{\prime \prime}\right)\) trois vecteurs de l'espace muni d'une base \((\vec{i} ; \vec{j} ; \vec{k})\). Le déterminant des vecteurs \(\vec{u}, \vec{v}\) et \(\vec{w}\) dans cet ordre est le réel noté \(\operatorname{det}(\vec{u} ; \vec{v} ; \vec{w})\) et défini par : |
Solution : Soient \(\vec{u}(x ; y ; z), \vec{v}\left(x^{\prime} ; y^{\prime} ; z^{\prime}\right)\) et \(\vec{w}\left(x^{\prime \prime} ; y^{\prime \prime} ; z^{\prime \prime}\right)\) trois vecteurs de l'espace muni d'une base \((\vec{i} ; \vec{j} ; \vec{k})\). Le déterminant des vecteurs \(\vec{u}, \vec{v}\) et \(\vec{w}\) dans cet ordre est le réel noté \(\operatorname{det}(\vec{u} ; \vec{v} ; \vec{w})\) et défini par :
|
Commentaires
Subscribe to Our Newsletter
Additional Links
Login Register Contact Certificate Validation Become Instructor About Terms and PoliciesContact
Reply to Comment